KONVERSI DARI NFA KE DFA
Penulis : D4985 – Novita Hanafiah, S.Kom.,M.Sc.
Sebuah diagram NFA dapat dikonversi menjadi DFA dengan membuat table transisi yang baru berdasarkan analisa dari transisi pada NFA. Perhatikan contoh berikut ini.
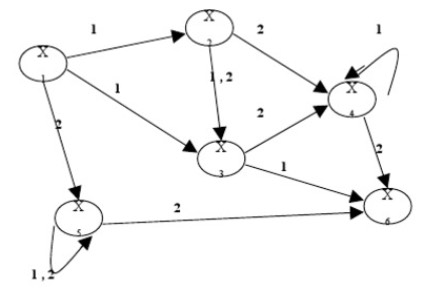
Jika diberikan sebuah NFA seperti pada gambar diatas dengan X1 sebagai state awal (Start state) dan X6 sebagai state akhir (final state). Alphabet yang digunakan pada NFA tersebut adalah {1,2} dan berikut ini adalah tabel transisi dari diagram tersebut.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
| X2 | X3 | {X3, X4} |
| X3 | X6 | X4 |
| X4 | X4 | X6 |
| X5 | X5 | {X5, X6} |
| *X6 | – | – |
Biasanya pada tabel transisi untuk menandakan sebuah start state diberikan dengan tanda panah, dan untuk final state ditandakan dengan tanda *. Setelah kita mengetahui tabel transisi dari NFA maka kita akan membuat tabel transisi dari DFA tersebut.
Pada awalnya start state pada DFA akan sama dengan start state di NFA, yaitu X1. Kita lihat bahwa transisi dari state X1 jika diberikan input 1 maka akan menuju ke 2 states yang berbeda, yaitu X2 dan X3. Sedangkan jika diberikan input 2 maka akan menuju ke state X5 saja. Pada tahap awal tabel transisi dari DFA akan menjadi seperti berikut ini.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
Kita tahu bahwa yang membuat DFA dan NFA berbeda adalah arah transisi untuk input yang sama, dimana jika NFA maka boleh memiliki lebih dari 1 transisi untuk input yang sama, sedangkan DFA hanya boleh memiliki 1 transisi untuk input yang sama. Pada kasus ini kita tahu bawah X1 bila diberi input 1 maka dapat menuju ke 2 arah, yaitu state X2 dan X3. Ketika di DFA hal ini tidak diperbolehkan (mempunyai lebih dari 1 state untuk transisi yang sama) sehingga kita akan menganggap {X2, X3} sebagai sebuah state. Oleh karena itu langkah selanjutnya adalah kita akan mencari transisi dari state {X2, X3}. Untuk mencari transisi dari state baru kita tersebut (state gabungan dari X2 dan X3) maka kita akan melihat transisi dari masing-masing state. Jika melihat dari tabel transisi di NFA kita tahu bahwa X2 jika diberikan input 1 maka akan menuju X3 dan X3 jika diberikan input 1 akan menuju state X6, sehingga hasil dari transisi state {X2, X3} adalah gabungan dari transisi state X2 dengan X3 yaitu {X3, X6}. Cara yang sama juga dilakukan untuk melihat hasil transisi dari state {X2,X3} jika diberikan input 2. Jika X2 diberikan input 2 maka akan menuju state {X3,X4} dan jika X3 diberikan input 2 maka akan menuju state X4, sehingga state {X2,X3} jika diberikan input 2 akan menuju state {X3, X4}. Berikut adalah transisi tabel dari pencarian transisi state {X2, X3}.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
| {X2, X3} | {X3, X6} | {X3, X4} |
Setelah mencari transisi untuk state {X2,X3} berikutnya adalah mencari transisi dari X5 (hasil dari transisi X1 jika diberikan input 2). Karena state X5 adalah 1 state sendiri di NFA juga maka hasil transisi dari X5 di DFA akan sama dengan transisi di NFA.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
| {X2, X3} | {X3, X6} | {X3, X4} |
| X5 | X5 | {X5, X6} |
Jika kita lihat tabel transisi DFA saat ini sudah ada 3 state yang kita cari transisinya yaitu X1, {X2,X3} dan {X5}. Kita lihat bahwa state {X2,X3} jika diberikan input 1 maka akan menuju ke state {X3, X6} dan seperti penjelasan sebelumnya bahwa di DFA tidak diijinkan untuk memiliki transisi lebih dari 1 untuk input yang sama, maka kita akan menganggap bahwa state {X3, X6} adalah sebuah state (State baru lagi). Demikian juga untuk state {X3, X4} merupakan sebuah state hasil dari transisi {X2, X3} jika diberikan input 2. Langkah berikutnya kita akan mencari transisi dari state {X3,X6} dan {X3,X4}.
Transisi X3 jika diberikan input 1 adalah X6 dan transisi X6 jika diberikan input 1 tidak akan menuju state manapun sehingga transisi dari state {X3, X6} untuk input 1 adalah X6 saja. Transisi X3 jika diberikan input 2 adalah X4 dan transisi X6 jika diberikan input 2 tidak akan menuju state manapun sehingga transisi dari state {X3, X6} jika diberikan input 2 adalah X4 saja.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
| {X2, X3} | {X3, X6} | {X3, X4} |
| X5 | X5 | {X5, X6} |
| {X3, X6} | X6 | X4 |
Transisi X3 jika diberikan input 1 adalah X6 dan transisi X4 jika diberikan input 1 adalah X4 sehingga transisi dari {X3,X4} jika diberikan input 1 adalah {X6, X4}. Transisi X3 jika diberikan input 2 adalah X4 dan transisi X4 jika diberikan input 2 adalah X6 sehingga transisi dari {X3,X4} jika diberikan input 2 adalah {X4, X6}.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
| {X2, X3} | {X3, X6} | {X3, X4} |
| X5 | X5 | {X5, X6} |
| {X3, X6} | X6 | X4 |
| {X3, X4} | {X6, X4} | {X4, X6} |
Proses pencarian transisi akan terus berulang sampai seluruh state sudah memiliki transisinya. Bisa dilihat pada tabel diatas untuk saat ini kita sudah memiliki 5 buah transisi state namun masih ada state yang belum ada transisinya ( yang ditandai dengan highlight kuning). Maka langkah berikutnya adalah kita masih perlu mencari transisi untuk state {X5, X6}, X6, X4, dan {X4,X6}. State {X4, X6} adalah sama dengan state {X6, X4} karena itu hanya penamaan saja yang terpenting adalah himpunan statenya tetap sama.
Setelah pencarian semua state maka akan diperoleh tabel transisi DFA sebagai berikut.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
| {X2, X3} | {X3, X6} | {X3, X4} |
| X5 | X5 | {X5, X6} |
| {X3, X6} | X6 | X4 |
| {X3, X4} | {X6, X4} | {X4, X6} |
| {X5, X6} | X5 | {X5, X6} |
| X6 | – | – |
| X4 | X4 | X6 |
| {X4, X6} | X4 | X6 |
Final state pada DFA adalah state di DFA yang mengandung final state di NFA. Pada contoh final state di NFA adalah X6, sehingga semua state di DFA yang mengandung state X6 menjadi final state di DFA.
| State | 1 | 2 |
| -> X1 | {X2, X3} | X5 |
| {X2, X3} | {X3, X6} | {X3, X4} |
| X5 | X5 | {X5, X6} |
| *{X3, X6} | X6 | X4 |
| {X3, X4} | {X6, X4} | {X4, X6} |
| *{X5, X6} | X5 | {X5, X6} |
| *X6 | – | – |
| X4 | X4 | X6 |
| *{X4, X6} | X4 | X6 |



Comments :